Big O Notation

고등학교 때를 생각해보면 수학의 정석 1단원인 집합 부분은 모두 열심히 공부했다.

수학의 집합, 한국사의 선사시대가 있다면 자료구조에는 빅오가 있는걸까 ㅎ 

 

제발 느리더라도 끝까지 가기를 바라면서 너무 열심히 쓰지는 말아야지.

 

빅오를 1줄로 요약해서 결론부터 생각해본다면, 어떤 것의 추세라고 요약하고싶다.

 

그리고 그 어떤 것에 대해 설명해보면 (어떤 것 -> 시간복잡도, 공간복잡도)

어떤 알고리즘이 효율적인가를 판단할 때, 크게 시간복잡도와 공간복잡도를 기준으로 판단하는데, 그것들이 얼만큼 효율적인가를 보기 쉽게 나타내주는 것이 빅오 표기법! 

 

빅오 표기법을 처음 봤을 때 너무 간단해서 더 어렵게 느껴졌다.

첫인상: O(1) 👀 이게뭔데. 뭐이렇게 많이 요약되어있는데

 

그런데 요약!! 그게 빅오 표기법의 뽀인트였다.

 

만약 어떤 n을 넣으면 for문을 돌아 n*2를 콘솔로 찍는 함수가 있다고 생각해보면 

const hi = (n) => {
	for (let i=0; i < n; i++) {
    	console.log(i);
    }
}

 

for문이 하나 있고, n의 크키만큼 콘솔이 찍히니까 요건 n 만큼 비례하면서 시간복잡도의 그래프가 그려질 것이다. O(n)

 

근데 만약 

const hihi = (n) => {
	for (let i=0; i < n; i++) {
    	console.log(i);
    }
	    for (let j=0; j < n; j++) {
    	console.log(j);
    }
}

요롷게 생겼다면 for 문이 2개니까 2n 이라고 생각할 수 있다. 하지만 빅오 표기법으로는 O(2n) 이라고 안하고 그냥 O(n)이라고 한다.

 

왜냐면 첫 번째 hi 함수에 n에 1을 넣을때 ~ n에 1000000을 넣을 때 까지 생각해보면 그래프가 직선의 모양으로 올라가는 모양이 된다.

그런데 두 번째 hihi 함수에 n에 1을 넣을 때 ~ n에 1000000 을 넣을 때 까지도 그래프가 조금 더 가파른 직선 모양을 그리며 올라간다.

 

두개의 기울기가 다르지만 둘 다 직선이다. 

 

이미지 출처

 

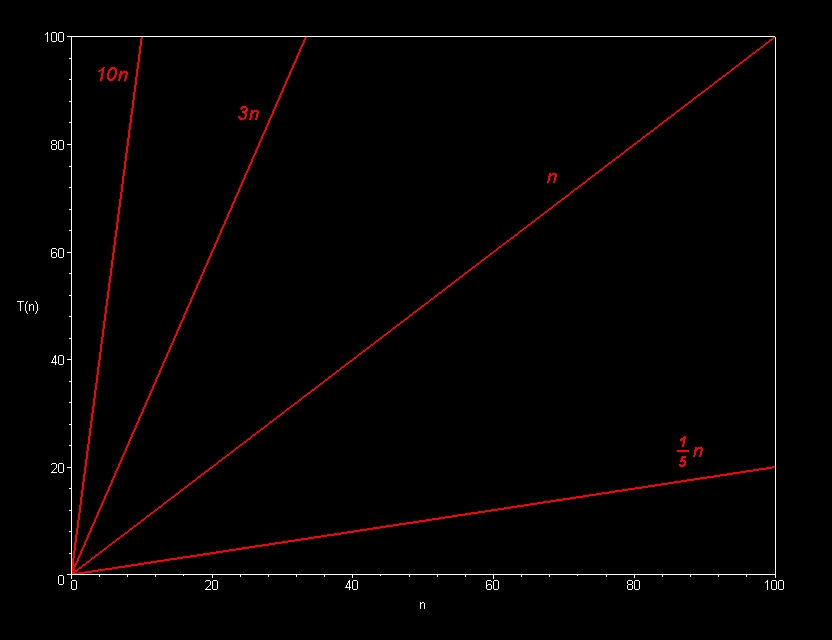
사실 나도 공부하고 사진 가져오면서 직접 이렇게보니 너무 다른데 라고 생각해서 뜨끔했지만, n의 예시가 작아서 그런것이고 모양은 직선으로 똑같다.

 

그래도 의심이 좀 들지만 다른 그래프를 보니 마음이 편안해졌다. (다행)

 

O(n^2)의 그래프를 보니 뒤에 작은 값 (100n + 500)은 결국 별로 큰 영향을 주지 않는다. 

 

둘 다 완만하게 올라가는 곡선의 모양을 하고있다. 

 

 

그래서 결국 아래와 같은 빅오 표기법들이 나눠지게 되었고, 보면 다 단순하게 생겼다. (나무위키)

나무위키 캡쳐

사진 출처

 

아 그리고 이 사진 가져오면서 생각난건데, Y축을 보면 Number of Operation 이라고 되어있다.

 

알고리즘 문제를 풀면 시간이 얼마나 걸리는지 초가 나온다. 그런데 그런 초들은 꾸진컴터 좋은컴터에 따라 다르게 나올 수 있고, 같은 컴퓨터에서 똑같은 함수를 여러번 돌린다면 초가 바뀐다. 

하지만 어느 환경에서든지 같은 함수를 돌리면 연산의 갯수는 항상 같다. 

 

그래서 빅오표기법은 연산의 갯수를 측정한다. 이거 그래듀 중요한건데 까묵을뻔.